Le théorème de la pizza

Vous avez déjà essayé de couper des parts de pizza parfaitement équitables ? Alors vous comprenez ce qui a motivé les mathématiciens Rick Mabry et Paul Deiermann. Ces deux chercheurs américains sont partis du principe que les pizzas étaient rarement coupées en leur centre et qu'il fallait, dès lors, trouver un moyen pour satisfaire ceux qui partagent la même pizza.

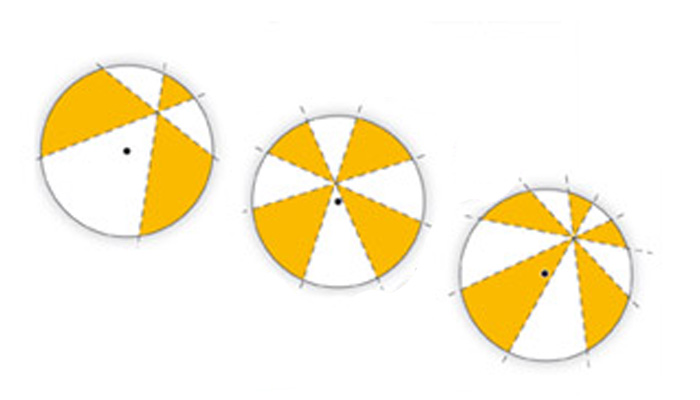
Il leur a fallu 11 années de réflexion pour aboutir à une règle mathématique qui permet de connaître la plus grande quantité de pizza par convive, quand aucune ligne de coupe ne passe par le centre. Il faut toutefois que chaque ligne de coupe passe par un même point et que chaque consommateur prenne une part contigüe à celle qui vient d'être prise.

Car il est relativement facile de diviser une pizza pour deux personnes en parts égales, indépendamment du nombre de fois qu’on la coupe, du moment que la ligne de coupe passe au moins une fois par le centre. Mais tout se complique quand la roulette à pizza oublie de bien passer au milieu.

C'est là que la formule de nos deux têtes pleines trouve tout son sens. Avec 4 lignes de coupe (ou tout nombre pair), les quantités par personnes sont égales. Avec 3 lignes de coupe (ou 7, 11, 15...), celui qui prend la part où se trouve le centre mangera plus de pizza. Avec 5 lignes de coupes (ou 9, 13, 17...), celui qui prend la part où se trouve le centre en mangera le moins.

Notons que ce théorème n'a aucune application dans le monde réel, mais, comme le souligne les deux chercheurs, « la beauté des résultats suffit en elle-même ».